–Я–µ—А–µ–Ї—А–µ—Б–љ—Л–є –Р.–°.
–Ь–µ—В–Њ–і –С–∞–є–µ—Б–∞, –њ—А–Є–Љ–µ–љ–Є—В–µ–ї—М–љ–Њ –Ї –∞—В–µ–Є–Ј–Љ—Г.
–Я–Њ –Љ–Њ—В–Є–≤–∞–Љ —Б—В–∞—В—М–Є –Я–Є—В–µ—А–∞ –Ф. –£–Є–ї—Б–Њ–љ–∞
–Ь–µ—В–Њ–і –С–∞–є–µ—Б–∞ —Н—В–Њ –∞–љ–∞–ї–Є—В–Є—З–µ—Б–Ї–Є–є –Љ–µ—В–Њ–і, –Ї–Њ—В–Њ—А—Л–є –Њ—З–µ–љ—М –њ–Њ–ї–µ–Ј–µ–љ –њ—А–Є —Б—А–∞–≤–љ–µ–љ–Є–Є –≥–Є–њ–Њ—В–µ–Ј. –Т —Н—В–Њ–Љ –Љ–µ—В–Њ–і–µ –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є –≤—Б–µ—Е –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е –Є—Б—Е–Њ–і–Њ–≤ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞ –Њ–±—К–µ–і–Є–љ—П—О—В—Б—П —Б –≥–Є–њ–Њ—В–µ–Ј–∞–Љ–Є, –Є–Ј–≤–µ—Б—В–љ—Л–Љ–Є –і–Њ –њ—А–Њ–≤–µ–і–µ–љ–Є—П —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞, –Є –Ј–∞—В–µ–Љ –Є—Б—З–Є—Б–ї—П–µ—В—Б—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–Њ–≥–Њ, —З—В–Њ –і–∞–љ–љ—Л–µ –≥–Є–њ–Њ—В–µ–Ј—Л –њ–Њ–і—В–≤–µ—А–і—П—В—Б—П –≤ —Е–Њ–і–µ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞.
–Ь–µ—В–Њ–і –Є—Б—З–µ—А–њ—Л–≤–∞—О—Й–µ –Њ–њ–Є—Б—Л–≤–∞–µ—В—Б—П —В–µ–Њ—А–µ–Љ–Њ–є –С–∞–є–µ—Б–∞:
p(Hi|I) * p(Ui|HiI) |
|
| p(Hi|UiI)= | |
p(Ui|I) |
–≥–і–µ:
p(Hi|I) - –љ–∞—З–∞–ї—М–љ–∞—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–Њ–≥–Њ, —З—В–Њ –≥–Є–њ–Њ—В–µ–Ј–∞ H –≤–µ—А–љ–∞, –Є—Б—Е–Њ–і—П –Є–Ј –Є–Љ–µ—О—Й–µ–≥–Њ—Б—П –Њ–њ—Л—В–∞ I;
p(Ui|I) - –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –љ–∞–±–ї—О–і–µ–љ–Є—П —Б–Њ–±—Л—В–Є—П Ui, –Є—Б—Е–Њ–і—П —В–Њ–ї—М–Ї–Њ –Є–Ј –Њ–њ—Л—В–∞ I.
p(Ui|HiI) - –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –љ–∞–±–ї—О–і–µ–љ–Є—П —Б–Њ–±—Л—В–Є—П Ui, –Є—Б—Е–Њ–і—П –Ї–∞–Ї –Є–Ј –Њ–њ—Л—В–∞ I, —В–∞–Ї –Є –Є–Ј –≥–Є–њ–Њ—В–µ–Ј—Л Hi.
p(Hi|UiI) - –њ–Њ—Б—В–µ—А–Є–Њ—А–љ–∞—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Є—Б—В–Є–љ–љ–Њ—Б—В–Є –≥–Є–њ–Њ—В–µ–Ј—Л Hi –љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –Њ–њ—Л—В–∞ I –Є –њ–Њ–ї—Г—З–µ–љ–љ—Л—Е —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л—Е –љ–∞–±–ї—О–і–µ–љ–Є–є Ui
–Ф–∞–≤–∞–є—В–µ –≤—Л–і–≤–Є–љ–µ–Љ –≥–Є–њ–Њ—В–µ–Ј—Л: "–Ъ–Њ—А–Њ–≤–∞ –Љ–Њ–ґ–µ—В –ї–µ—В–∞—В—М"(H1=R) –Є "–Ъ–Њ—А–Њ–≤–∞ –љ–µ –Љ–Њ–ґ–µ—В –ї–µ—В–∞—В—М"(H1=notR),
—З—В–Њ–±—Л –њ—А–Њ–Є–ї–ї—О—Б—В—А–Є—А–Њ–≤–∞—В—М —А–∞–±–Њ—В—Г –Љ–µ—В–Њ–і–∞.
–Ф–Њ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞ –Њ—Ж–µ–љ–Є–Љ –∞–њ—А–Є–Њ—А–љ—Г—О –і–Њ—Б—В–Њ–≤–µ—А–љ–Њ—Б—В—М –Ї–∞–ґ–і–Њ–є –Є–Ј –≥–Є–њ–Њ—В–µ–Ј.
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –Ї–Њ—А–Њ–≤–∞ –ї–Є–±–Њ —Б–њ–Њ—Б–Њ–±–љ–∞ –ї–µ—В–∞—В—М, –ї–Є–±–Њ –љ–µ—Б–њ–Њ—Б–Њ–±–љ–∞, —Б—Г–Љ–Љ–∞ –≤–µ—А–Њ—П—В–љ–Њ—Б—В–µ–є –Є—Б—В–Є–љ–љ–Њ—Б—В–Є –Њ–±–µ–Є—Е –≥–Є–њ–Њ—В–µ–Ј —Б–Њ—Б—В–∞–≤–ї—П–µ—В –µ–і–Є–љ–Є—Ж—Г. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –ї–µ—В–∞—О—Й–∞—П –Ї—А—Г–≥–∞–Љ–Є –Ї–Њ—А–Њ–≤–∞ –њ–Њ—Б—В–∞–≤–Є–ї–∞ –±—Л –њ–Њ–і —Б–Њ–Љ–љ–µ–љ–Є–µ –Т–°–Х, —З—В–Њ –Љ—Л –Ј–љ–∞–µ–Љ –Њ –њ–Њ–ї–µ—В–∞—Е, –Њ—Ж–µ–љ–Є–Љ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –љ–∞–ї–Є—З–Є—П –ї–µ—В–∞—В–µ–ї—М–љ—Л—Е —Б–њ–Њ—Б–Њ–±–љ–Њ—Б—В–µ–є —Г –Ї–Њ—А–Њ–≤, –Ї–∞–Ї –Ї—А–∞–є–љ–µ –Љ–∞–ї—Г—О, —Е–Њ—В—П –Є –љ–µ–љ—Г–ї–µ–≤—Г—О –≤–µ–ї–Є—З–Є–љ—Г R. –Э—Г–ї–µ–≤—Г—О –≤–µ–ї–Є—З–Є–љ—Г –љ–∞–Ј–љ–∞—З–Є—В—М –љ–µ–ї—М–Ј—П –і–Њ —В–µ—Е –њ–Њ—А, –њ–Њ–Ї–∞ –Љ—Л –љ–µ –±—Г–і–µ–Љ –Ј–љ–∞—В—М –Т–°–Х –Њ –Т–°–Х–• –≤–Є–і–∞—Е –њ–Њ–ї–µ—В–Њ–≤.
P(H1|I) = R; R ~ 0;
–†–∞–Ј—Г–Љ–µ–µ—В—Б—П, –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Њ—В—Б—Г—Б—В–≤–Є—П –ї–µ—В–∞—В–µ–ї—М–љ—Л—Е —Б–њ–Њ—Б–Њ–±–љ–Њ—Б—В–µ–є —Г –Ї–Њ—А–Њ–≤ —Б–Њ—Б—В–∞–≤–Є—В –±–ї–Є–Ј–Ї—Г—О –Ї –µ–і–Є–љ–Є—Ж–µ –≤–µ–ї–Є—З–Є–љ—Г 1-R –Є–ї–Є notR.
P(H2|I) = 1-R; 1-R ~ 1;
–Ю—Ж–µ–љ–Є–Љ –∞–њ—А–Є–Њ—А–љ—Г—О –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Њ–±–Њ–Є—Е –Є—Б—Е–Њ–і–Њ–≤ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞, –Є—Б—Е–Њ–і—П –Є–Ј –Є–Љ–µ—О—Й–µ–≥–Њ—Б—П –Њ–њ—Л—В–∞. –≠—В–∞ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –≤—Л—З–Є—Б–ї—П–µ—В—Б—П, –Ї–∞–Ї –і–Њ–ї—П –Ї–∞–ґ–і–Њ–≥–Њ –Є–Ј –Є—Б—Е–Њ–і–Њ–≤ –≤ —Г–ґ–µ –Є–Љ–µ—О—Й–Є—Е—Б—П –љ–∞–±–ї—О–і–µ–љ–Є—П—Е. –Ф–ї—П –њ–Њ–ї–µ—В–∞ –Ї–Њ—А–Њ–≤—Л (U1) —В–∞–Ї–∞—П –і–Њ–ї—П —А–∞–≤–љ–∞ –љ—Г–ї—О, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –љ–Є–Ї–Њ–≥–і–∞ —А–∞–љ–µ–µ –ї–µ—В–∞—О—Й–∞—П –Ї–Њ—А–Њ–≤–∞ –љ–µ –љ–∞–±–ї—О–і–∞–ї–∞—Б—М, –љ–Њ —З–µ–Љ —З–µ—А—В –љ–µ —И—Г—В–Є—В:
P(U1|I) = 0;
–°–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, –≤—Б–µ –Є–Ј–≤–µ—Б—В–љ—Л–µ –љ–∞–Љ –Ї–Њ—А–Њ–≤—Л –љ–µ –ї–µ—В–∞–ї–Є, –Є –і–Њ–ї—П –ї–µ—В–∞–ї—М–љ—Л—Е –Є—Б—Е–Њ–і–Њ–≤ (U2) –Њ—Е–≤–∞—В—Л–≤–∞–µ—В –≤–µ—Б—М –Њ–±—К–µ–Љ –љ–∞–±–ї—О–і–µ–љ–Є–є I:
P(U2|I) = 1;
–Ґ–µ–њ–µ—А—М, –Њ—Ж–µ–љ–Є–Љ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –і–≤—Г—Е –Є—Б—Е–Њ–і–Њ–≤ –љ–∞ –Њ—Б–љ–Њ–≤–µ –Ї–∞–Ї –Њ–њ—Л—В–∞, —В–∞–Ї –Є –≥–Є–њ–Њ—В–µ–Ј. –Э–∞—З–љ–µ–Љ —Б–Њ –≤—В–Њ—А–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л(–Њ –љ–µ—Б–њ–Њ—Б–Њ–±–љ–Њ—Б—В–Є –Ї–Њ—А–Њ–≤ –Ї –њ–Њ–ї–µ—В—Г). –Ф–∞–љ–љ—Л–є —Б–ї—Г—З–∞–є –±–Њ–ї–µ–µ –њ—А–Њ—Б—В. –У–Є–њ–Њ—В–µ–Ј–∞ (H2) —Г—В–≤–µ—А–ґ–і–∞–µ—В, —З—В–Њ –Ї–Њ—А–Њ–≤–∞ –њ–Њ–≥–Є–±–љ–µ—В –±–µ–Ј—Г—Б–ї–Њ–≤–љ–Њ, –Є –њ—А–µ–і—И–µ—Б—В–≤—Г—О—Й–Є–є –Њ–њ—Л—В (I) —Н—В–Њ–Љ—Г –љ–µ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є—В. –Я–Њ—Н—В–Њ–Љ—Г –ї–µ—В–∞—В–µ–ї—М–љ—Л–є –Є—Б—Е–Њ–і (U1) –≤ —А–∞–Љ–Ї–∞—Е –і–∞–љ–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л (H2) –Є–Љ–µ–µ—В –љ—Г–ї–µ–≤—Г—О –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М:
P(U1|H2I) = 0;
–†–∞–Ј—Г–Љ–µ–µ—В—Б—П, –ї–µ—В–∞–ї—М–љ—Л–є –Є—Б—Е–Њ–і (U2) –≤ —А–∞–Љ–Ї–∞—Е –і–∞–љ–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л (H2) –±–µ–Ј—Г—Б–ї–Њ–≤–µ–љ, –Є –Є–Љ–µ–µ—В –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —А–∞–≤–љ—Г—О –µ–і–Є–љ–Є—Ж–µ:
P(U2|H2I) = 1;
–Т —Б–ї—Г—З–∞–µ –≥–Є–њ–Њ—В–µ–Ј—Л –Њ –ї–µ—В–∞–љ–Є–Є –Ї–Њ—А–Њ–≤ –Љ—Л –Є–Љ–µ–µ–Љ –±–Њ–ї–µ–µ —Б–ї–Њ–ґ–љ—Л–є —Б–ї—Г—З–∞–є. –Т—Л—З–Є—Б–ї–Є—В—М –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –≤—Л–ґ–Є–≤–∞–љ–Є—П –Ї–Њ—А–Њ–≤—Л –≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ –љ–µ —В–∞–Ї –њ—А–Њ—Б—В–Њ. –Ю–±—Б—В–Њ—П—В–µ–ї—М—Б—В–≤–∞ –Љ–Њ–≥—Г—В –њ–Њ–Љ–µ—И–∞—В—М –Ї–Њ—А–Њ–≤–µ –њ–Њ–Ї–∞–Ј–∞—В—М —Б–µ–±—П –≤–Њ –≤—Б–µ–є –Ї—А–∞—Б–µ. –Ъ–Њ—А–Њ–≤–∞ –Љ–Њ–ґ–µ—В –њ–Њ–≥–Є–±–љ—Г—В—М –Є–Ј-–Ј–∞ –љ–µ–ї–µ—В–љ–Њ–є –њ–Њ–≥–Њ–і—Л, –Є–ї–Є –Є–Ј-–Ј–∞ –≤–љ–µ–Ј–∞–њ–љ–Њ –њ—А–Њ—П–≤–Є–≤—И–µ–є—Б—П —В—П–≥–Є –Ї —Б–∞–Љ–Њ—Г–±–Є–є—Б—В–≤—Г. –Ш–ї–Є –≤—А–∞–ґ–µ—Б–Ї–Є–µ –і–Є–≤–µ—А—Б–∞–љ—В—Л –≤–њ—А—Л—Б–љ—Г—В –Ї–Њ—А–Њ–≤–µ —П–і –≤ –ї–µ—В–∞—В–µ–ї—М–љ—Г—О –Љ—Л—И—Ж—Г. –Э–Њ –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г —Г –љ–∞—Б –њ–Њ –њ—А–µ–ґ–љ–µ–Љ—Г –≤—Б–µ–≥–Њ –і–≤–∞ –≤–µ—А–Њ—П—В–љ—Л—Е –Є—Б—Е–Њ–і–∞, —А–∞–Ј–і–µ–ї–Є–Љ –Њ–±—Й—Г—О –µ–і–Є–љ–Є—З–љ—Г—О –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Љ–µ–ґ–і—Г —Н—В–Є–Љ–Є –і–≤—Г–Љ—П –Є—Б—Е–Њ–і–∞–Љ–Є –њ–Њ—А–Њ–≤–љ—Г.
P(U1|H1I) = 0.5; // –Я–Њ–ї–µ—В–µ–ї–∞
P(U2|H1I) = 0.5; // –Я–Њ–≥–Є–±–ї–∞
–Ш—В–∞–Ї, —Д–Є—Д—В–Є-—Д–Є—Д—В–Є. –Ч–∞–Љ–µ—З—Г, —З—В–Њ —Н—В–Њ –µ—Й–µ –Њ—З–µ–љ—М –њ—А–Є–ї–Є—З–љ—Л–µ —И–∞–љ—Б—Л. –Т–Њ—В —В–Њ–ї—М–Ї–Њ –Ї–Њ—А–Њ–≤—Г –њ–Њ—З–µ–Љ—Г-—В–Њ –ґ–∞–ї–Ї–Њ.
–Ш—В–∞–Ї, –њ—А–µ–і–≤–∞—А–Є—В–µ–ї—М–љ—Л–є —Н—В–∞–њ –Ј–∞–≤–µ—А—И–µ–љ. –Ф–∞–≤–∞–є—В–µ —А–∞–Ј—А–∞–±–Њ—В–∞–µ–Љ –Љ–µ—В–Њ–і–Є–Ї—Г —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ: —Б–µ—А–Є—П –Ї–Њ—А–Њ–≤ —Б–±—А–∞—Б—Л–≤–∞–µ—В—Б—П —Б –≤–µ—А—В–Њ–ї–µ—В–∞. –Т—Л—Б–Њ—В–∞ вАУ 1–Ї–Љ.
–Я—А–Є —Н—В–Њ–Љ –њ–Њ–і—Б—З–Є—В—Л–≤–∞–µ—В—Б—П —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ –ї–µ—В–∞–ї—М–љ—Л—Е –Є –ї–µ—В–∞—В–µ–ї—М–љ—Л—Е –Є—Б—Е–Њ–і–Њ–≤. –Х–і–Є–љ—Б—В–≤–µ–љ–љ—Л–Љ —Б–≤–Є–і–µ—В–µ–ї—М—Б—В–≤–Њ–Љ —Б–њ–Њ—Б–Њ–±–љ–Њ—Б—В–Є –Ї–Њ—А–Њ–≤ –Ї –њ–Њ–ї–µ—В—Г –±—Г–і–µ–Љ —Б—З–Є—В–∞—В—М –љ–∞–±–ї—О–і–µ–љ–Є–µ –ї–µ—В—П—Й–µ–є –Ї–Њ—А–Њ–≤—Л. –Я–Њ–і—А–∞–Ј—Г–Љ–µ–≤–∞–µ—В—Б—П –њ–Њ–ї–µ—В –≥–Њ—А–Є–Ј–Њ–љ—В–∞–ї—М–љ—Л–є –Є–ї–Є –њ–Њ –≤–Њ—Б—Е–Њ–і—П—Й–µ–є, –±–µ–Ј –њ—А–Є–Љ–µ–љ–µ–љ–Є—П —В–µ—Е–љ–Є—З–µ—Б–Ї–Є—Е —Б—А–µ–і—Б—В–≤.
/* –Ь–∞–ї–µ–љ—М–Ї–∞—П –њ—А–µ–і–Њ—Б—В–Њ—А–Њ–ґ–љ–Њ—Б—В—М –Њ—В –Ї–Њ—А–Њ–≤ —Б –њ–∞—А–∞—И—О—В–∞–Љ–Є –Є –Љ–Њ—В–Њ—А—З–Є–Ї–∞–Љ–Є a-la –Ъ–∞—А–ї—Б—Б–Њ–љ */
–Ґ–µ–њ–µ—А—М –њ—А–Є—Б—В—Г–њ–∞–µ–Љ –Ї —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В—Г (–њ—А–Є–≥–ї–∞—И–µ–љ–љ—Л–є –Њ—А–Ї–µ—Б—В—А –Є–≥—А–∞–µ—В —В—А–∞—Г—А–љ—Л–є –Љ–∞—А—И).
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –Њ–±–∞ –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е –Є—Б—Е–Њ–і–∞:
–Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ, –Њ–і–љ–∞ –Є–Ј –Ї–Њ—А–Њ–≤–Њ–Ї, –њ–ї–∞–≤–љ–Њ —А–∞–Ј–≤–µ—А–љ—Г–≤—И–Є—Б—М –Є –Љ—П–≥–Ї–Њ –Ї–Њ—Б–љ—Г–≤—И–Є—Б—М –Ј–µ–Љ–ї–Є, –њ–Њ—Б–ї–µ –Ї–Њ—А–Њ—В–Ї–Њ–є –њ—А–Њ–±–µ–ґ–Ї–Є –Ј–∞–Љ–Є—А–∞–µ—В —Г —Б—В–Њ–ї–∞, –Ј–∞ –Ї–Њ—В–Њ—А—Л–Љ –Ј–∞—Б–µ–і–∞–µ—В –Ї–Њ–Љ–Є—Б—Б–Є—П –њ–Њ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—О —Б–≤–µ—А—Е—Ж–µ–љ–љ—Л—Е –≥–Є–њ–Њ—В–µ–Ј.
–Я–Њ—Б–ї–µ —В–∞–Ї–Њ–≥–Њ –Є—Б—Е–Њ–і–∞ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞, –њ–Њ—Б—В–µ—А–Є–Њ—А–љ–∞—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Є—Б—В–Є–љ–љ–Њ—Б—В–Є –≥–Є–њ–Њ—В–µ–Ј—Л –Њ –њ—А–Є–Ј–µ–Љ–ї–µ–љ–љ–Њ–є —Б—Г—Й–љ–Њ—Б—В–Є –Ї–Њ—А–Њ–≤—Л, –љ–µ–Љ–µ–і–ї–µ–љ–љ–Њ –Њ–±—А–∞—В–Є—В—Б—П –≤ –љ–Њ–ї—М:
p(H2=–љ–µ—Б–њ–Њ—Б–Њ–±–љ–∞ | –∞ –Њ–љ–∞ U1=–ї–µ—В–∞–µ—В, —Е–Њ—В—П I=—А–∞–љ—М—И–µ –љ–µ –ї–µ—В–∞–ї–∞) = 0, –Є–ї–Є –±–Њ–ї–µ–µ —Д–Њ—А–Љ–∞–ї—М–љ–Њ:
P(H2|I) * P(U1|H2I) |
~1 * 0 | |||
| P(H2|U1I) = | = | =0 | ||
P(U1|I) |
0 |
–Р –≤—Б–µ –њ–Њ—В–Њ–Љ—Г, —З—В–Њ –∞–њ—А–Є–Њ—А–љ–∞—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –њ–Њ–ї–µ—В–∞ –і–ї—П –і–∞–љ–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л –±—Л–ї–∞ –љ—Г–ї–µ–≤–Њ–є:
p(U1|H2I) = 0.
–Я–Њ—Б—В–µ—А–Є–Њ—А–љ–∞—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л –Њ—В–ї–Є—З–љ–∞ –Њ—В –љ—Г–ї—П –Є —А–∞–≤–љ–∞ –µ–і–Є–љ–Є—Ж–µ, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ—А–Є —В–∞–Ї–Њ–Љ —А–∞—Б–Ї–ї–∞–і–µ –Є—Б—В–Є–љ–љ–Њ—Б—В—М –і–∞–љ–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л –µ—Б—В—М –љ–µ–њ—А–µ–ї–Њ–ґ–љ—Л–є —Д–∞–Ї—В.
–Ю–і–љ–∞–Ї–Њ –і–∞–љ–љ—Л–є —А–∞—Б–Ї–ї–∞–і –µ—Б—В—М —В—А–Є–≤–Є–∞–ї—М–љ—Л–є, –Є –≤—Б–µ —Б—В–Њ–ї–Ї–љ–Њ–≤–µ–љ–Є—П –Є–і–µ–є, –≥–і–µ –Њ–љ —Б–ї—Г—З–Є–ї—Б—П, –і–∞–≤–љ–Њ –Є –Њ–Ї–Њ–љ—З–∞—В–µ–ї—М–љ–Њ –Ј–∞–Ї–Њ–љ—З–Є–ї–Є—Б—М –њ–Њ–±–µ–і–Њ–є –Њ–і–љ–Њ–є –Є–Ј –≥–Є–њ–Њ—В–µ–Ј. –Ь—Л –ґ–µ –Є–Љ–µ–µ–Љ –і–µ–ї–Њ —Б –≥–Њ—А–∞–Ј–і–Њ –±–Њ–ї–µ–µ —Б–ї–Њ–ґ–љ–Њ–є —Б–Є—В—Г–∞—Ж–Є–µ–є.
–Х—Б–ї–Є –Ї–Њ—А–Њ–≤–Ї–∞ —А–∞–Ј–Њ–±—М–µ—В—Б—П, –Њ–±–µ –≥–Є–њ–Њ—В–µ–Ј—Л –±—Г–і—Г—В –Є–Љ–µ—В—М –љ–µ–љ—Г–ї–µ–≤—Г—О –њ–Њ—Б—В–µ—А–Є–Њ—А–љ—Г—О –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –Њ–±–µ –Њ–љ–Є –і–Њ–њ—Г—Б–Ї–∞–ї–Є —В–∞–Ї–Њ–µ —А–∞–Ј–≤–Є—В–Є–µ —Б–Њ–±—Л—В–Є–є. –°–Є–ї–∞ –Љ–µ—В–Њ–і–∞ –С–∞–є–µ—Б–∞ –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ —В–Њ–Љ, —З—В–Њ –њ—А–Є —А–µ–Ј—Г–ї—М—В–∞—В–µ, –і–Њ–њ—Г—Б—В–Є–Љ–Њ–Љ –і–ї—П –Њ–±–µ–Є—Е –≥–Є–њ–Њ—В–µ–Ј, –Љ—Л —Б—В–∞–љ–µ–Љ –Њ–±–ї–∞–і–∞—В–µ–ї—П–Љ–Є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ–є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є –Є—Б—В–Є–љ–љ–Њ—Б—В–Є –і–≤—Г—Е –≥–Є–њ–Њ—В–µ–Ј.
| P(H1|I) * P(U2|H1I) | ~0 * 0.5 | |||
| P(H1|U2I) = | = | = ~0; | ||
P(U2|I) |
1 |
| P(H2|I) * P(U2|H2I) | ~1 * 1 | |||
| P(H2|U2I) = | = | = ~1; | ||
P(U2|I) |
1 |
–І—В–Њ –ґ–µ –њ—А–Њ–Є–Ј–Њ—И–ї–Њ —Б –≤–µ—А–Њ—П—В–љ–Њ—Б—В—П–Љ–Є –Є—Б—В–Є–љ–љ–Њ—Б—В–Є –Њ–±–µ–Є—Е –≥–Є–њ–Њ—В–µ–Ј –њ–Њ—Б–ї–µ –≥–Є–±–µ–ї–Є –Ї–Њ—А–Њ–≤–Ї–Є? –Ш–Ј–Љ–µ–љ–Є–ї–Є—Б—М –ї–Є –Њ–љ–Є? –Р –µ—Б–ї–Є –і–∞, —В–Њ –Ї–∞–Ї?
–Ф–∞–≤–∞–є—В–µ —Б–і–µ–ї–∞–µ–Љ –њ—А–Њ—Б—В–Њ–µ —З–Є—Б–ї–µ–љ–љ—Л–є —А–∞—Б—З–µ—В.
–Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ, —З—В–Њ –Њ–±–µ –≥–Є–њ–Њ—В–µ–Ј—Л –њ—А–Є–Љ–µ—А–љ–Њ —А–∞–≤–љ–Њ—Ж–µ–љ–љ—Л –Є –Є–Љ–µ—О—В –∞–њ—А–Є–Њ—А–љ—Г—О –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Є—Б—В–Є–љ–љ–Њ—Б—В–Є –њ–Њ 0.5.
–Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ –і–∞–ґ–µ, —З—В–Њ –≤–µ—Б—М –Є–Љ–µ—О—Й–Є–є—Б—П –ґ–Є—В–µ–є—Б–Ї–Є–є –Њ–њ—Л—В –љ–µ –њ–Њ–Ј–≤–Њ–ї—П–µ—В –љ–∞–Љ –Њ—Ж–µ–љ–Є—В—М —И–∞–љ—Б—Л –Є—Б—Е–Њ–і–Њ–≤ –Є–љ–∞—З–µ, –Ї–∞–Ї —Д–Є—Д—В–Є/—Д–Є—Д—В–Є, —В–Њ-–µ—Б—В—М –њ–Њ 0.5
–†–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ –ґ–µ —И–∞–љ—Б–Њ–≤ –≤ —А–∞–Љ–Ї–∞—Е –≥–Є–њ–Њ—В–µ–Ј –Њ—Б—В–∞–≤–Є–Љ –±–µ–Ј –Є–Ј–Љ–µ–љ–µ–љ–Є–є, –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г —Н—В–Є —И–∞–љ—Б—Л вАУ –љ–µ–Њ—В—К–µ–Љ–ї–µ–Љ–∞—П —З–∞—Б—В—М –≥–Є–њ–Њ—В–µ–Ј.
–І–µ–Љ—Г –ґ–µ —А–∞–≤–љ–∞ –њ–Њ—Б—В–µ—А–Є–Њ—А–љ–∞—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –і–ї—П –Ї–∞–ґ–і–Њ–є –Є–Ј –≥–Є–њ–Њ—В–µ–Ј –њ–Њ—Б–ї–µ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞?
| 0.5 * 0.5 | ||
| P(H1|U2I) = | = 0.5; | |
0.5 |
| 0.5 * 1 | ||
| P(H2|U2I) = | = 1; | |
0.5 |
–Э–∞ —Н—В–Њ–Љ —Н—В–∞–њ–µ –Љ–Њ–ґ–љ–Њ –њ—А–Њ–≤–µ—Б—В–Є –љ–Њ—А–Љ–∞–ї–Є–Ј–∞—Ж–Є—О —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤, —Б —В–µ–Љ, —З—В–Њ–±—Л —Б—Г–Љ–Љ–∞ —Н—В–Є—Е –≤–µ—А–Њ—П—В–љ–Њ—Б—В–µ–є —Б–Њ—Б—В–∞–≤–ї—П–ї–∞ –µ–і–Є–љ–Є—Ж—Г. –≠—В–Њ, –≤ –Њ–±—Й–µ–Љ, –љ–µ –µ—Б—В—М –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ, –љ–Њ –≤ —В–µ–Њ—А–Є–Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–µ–є —В–∞–Ї —Г–ґ –њ—А–Є–љ—П—В–Њ. –Ь–Њ–ґ–µ—В–µ –Љ–љ–µ –њ–Њ–≤–µ—А–Є—В—М, —З—В–Њ –љ–Є–Ї–∞–Ї–Є—Е –њ–Њ–і–≤–Њ—Е–Њ–≤ —В—Г—В –љ–µ—В.
-
P(H1|U2I) |
0.5 |
|||
| P(H1|U2I) = | = | = 0.3333333333 | ||
| P(H1|U2I) + P(H2|U2I) | 0.5 + 1 |
| P(H2|U2I) | 1 |
|||
| P(H1|U2I) = | = | = 0.6666666666 | ||
| P(H1|U2I) + P(H2|U2I) | 0.5 + 1 |
–Ш—В–∞–Ї, –і–ї—П –њ–µ—А–≤–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Г–Љ–µ–љ—М—И–Є–ї–∞—Б—М, –∞ –і–ї—П –≤—В–Њ—А–Њ–є вАУ –≤–Њ–Ј—А–Њ—Б–ї–∞. –Э–µ—В—А—Г–і–љ–Њ –і–Њ–≥–∞–і–∞—В—М—Б—П, —З—В–Њ –њ—А–Є –Ї–∞–ґ–і–Њ–Љ –њ–Њ—Б–ї–µ–і—Г—О—Й–µ–Љ —Б–Љ–µ—А—В–µ–ї—М–љ–Њ–Љ –Є—Б—Е–Њ–і–µ, –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –≥–Є–њ–Њ—В–µ–Ј—Л –Њ –љ–µ–ї–µ—В–∞–љ–Є–Є –Ї–Њ—А–Њ–≤ –±—Г–і–µ —Б—В–∞–љ–Њ–≤–Є—В—М—Б—П –≤—Б–µ –≤—Л—И–µ –Є –≤—Л—И–µ, –∞ –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Њ–є вАУ –≤—Б–µ –љ–Є–ґ–µ –Є –љ–Є–ґ–µ. –Ь–Њ–ґ–µ—В –њ–Њ–Ї–∞–Ј–∞—В—М—Б—П —Г–і–Є–≤–Є—В–µ–ї—М–љ—Л–Љ, –љ–Њ –≤—Б–µ–≥–Њ –і–≤–∞–і—Ж–∞—В–Є –Ї–Њ—А–Њ–≤, –њ—А–Є–љ–µ—Б–µ–љ–љ—Л—Е –≤ –ґ–µ—А—В–≤—Г –љ–∞—Г–Ї–µ, –і–Њ—Б—В–∞—В–Њ—З–љ–Њ, —З—В–Њ–±—Л –≤—В–Њ—А–∞—П –≥–Є–њ–Њ—В–µ–Ј–∞ –Њ–Ї–∞–Ј–∞–ї–∞—Б—М –≤ –Ь–Ш–Ы–Ы–Ш–Ю–Э —А–∞–Ј –±–Њ–ї–µ–µ –≤–µ—А–Њ—П—В–љ–Њ–є, —З–µ–Љ –њ–µ—А–≤–∞—П. –Ш —Н—В–Њ –њ—А–Є —А–∞–≤–љ—Л—Е –љ–∞—З–∞–ї—М–љ—Л—Е —И–∞–љ—Б–∞—Е.
–Т–Њ—В –Ї–∞–Ї –≤—Л–≥–ї—П–і–Є—В –і–Є–љ–∞–Љ–Є–Ї–∞ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –Њ—В–љ–Њ—И–µ–љ–Є—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В–µ–є –і–ї—П –Њ–њ–Є—Б–∞–љ–љ–Њ–≥–Њ —Б–ї—Г—З–∞—П:
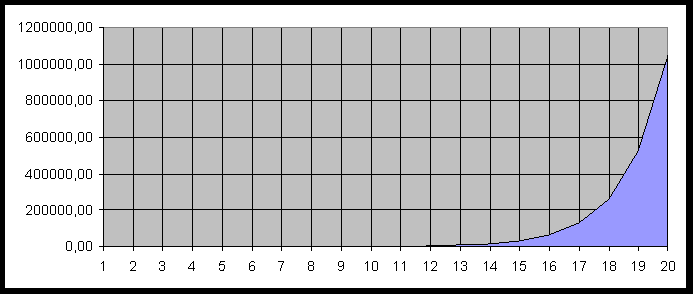
–Т—Б–µ —Б–Њ–Љ–љ–µ–≤–∞—О—Й–Є–µ—Б—П –Љ–Њ–≥—Г—В –њ—А–Њ–≤–µ—А–Є—В—М —Н—В–Є —А–µ–Ј—Г–ї—М—В–∞—В—Л –≤ –Ь–µ–ї–Ї–Њ—Б–Њ—Д—В–Њ–≤—Б–Њ–Љ –Б–Ї—Б–µ–ї–µ:
–†–∞—Б—З–µ—В–љ—Л–µ –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є |
–Э–Њ—А–Љ–∞–ї–Є–Ј–Њ–≤–∞–љ–љ—Л–µ –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є |
–Ю—В–љ–Њ—И–µ–љ–Є–µ –≤–µ—А–Њ—П—В–љ–Њ—Б—В–µ–є |
|||
–У–Є–њ–Њ—В–µ–Ј–∞ вДЦ1 |
–У–Є–њ–Њ—В–µ–Ј–∞ вДЦ2 |
–У–Є–њ–Њ—В–µ–Ј–∞ вДЦ1 |
–У–Є–њ–Њ—В–µ–Ј–∞ вДЦ2 |
||
–Р–њ—А–Є–Њ—А–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П |
0,5000 |
0,5000 |
0,5000 |
0,5000 |
1,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ1 |
0,5000 |
1,0000 |
0,3333 |
0,6667 |
2,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ2 |
0,3333 |
1,3333 |
0,2000 |
0,8000 |
4,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ3 |
0,2000 |
1,6000 |
0,1111 |
0,8889 |
8,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ4 |
0,1111 |
1,7778 |
0,0588 |
0,9412 |
16,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ5 |
0,0588 |
1,8824 |
0,0303 |
0,9697 |
32,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ6 |
0,0303 |
1,9394 |
0,0154 |
0,9846 |
64,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ7 |
0,0154 |
1,9692 |
0,0078 |
0,9922 |
128,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ8 |
0,0078 |
1,9845 |
0,0039 |
0,9961 |
256,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ9 |
0,0039 |
1,9922 |
0,0019 |
0,9981 |
512,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ10 |
0,0019 |
1,9961 |
0,0010 |
0,9990 |
1024,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ11 |
0,0010 |
1,9980 |
0,0005 |
0,9995 |
2048,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ12 |
0,0005 |
1,9990 |
0,0002 |
0,9998 |
4096,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ13 |
0,0002 |
1,9995 |
0,0001 |
0,9999 |
8192,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ14 |
0,0001 |
1,9998 |
0,0001 |
0,9999 |
16384,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ15 |
0,0001 |
1,9999 |
0,0000 |
1,0000 |
32768,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ16 |
0,0000 |
1,9999 |
0,0000 |
1,0000 |
65536,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ17 |
0,0000 |
2,0000 |
0,0000 |
1,0000 |
131072,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ18 |
0,0000 |
2,0000 |
0,0000 |
1,0000 |
262144,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ19 |
0,0000 |
2,0000 |
0,0000 |
1,0000 |
524288,00 |
–≠–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В вДЦ20 |
0,0000 |
2,0000 |
0,0000 |
1,0000 |
1048576,00 |
–Ъ–∞–Ї –≤–Є–і–љ–Њ –Є–Ј —В–∞–±–ї–Є—Ж—Л, —Г–ґ–µ –њ—П—В–љ–∞–і—Ж–∞—В—Л–є —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В –љ–Є–Ј–≤–Њ–і–Є—В –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –ї–µ—В–∞–љ–Є—П –Ї–Њ—А–Њ–≤ –і–Њ –љ—Г–ї—П, —Б —В–Њ—З–љ–Њ—Б—В—М—О –і–Њ —З–µ—В–≤–µ—А—В–Њ–≥–Њ –Ј–љ–∞–Ї–∞ –њ–Њ—Б–ї–µ –Ј–∞–њ—П—В–Њ–є. –Р —Е–∞—А–∞–Ї—В–µ—А –Ї—А–Є–≤–Њ–є –њ–Њ–і—Б–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –њ–Њ—Б–ї–µ —Г–±–Є–є—Б—В–≤–∞ —Б–Њ—В–Њ–є –љ–µ—Б—З–∞—Б—В–љ–Њ–є –Ї–Њ—А–Њ–≤–Ї–Є –Ј–љ–∞—З–∞—Й–µ–є —Ж–Є—Д—А–µ –≤ —Н—В–Њ–є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є –±—Г–і—Г—В –њ—А–µ–і—И–µ—Б—В–≤–Њ–≤–∞—В—М –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —Б–Њ—В–µ–љ –љ—Г–ї–µ–є.
–І—В–Њ –ґ–µ –Ј–∞ —А–µ–Ј—Г–ї—М—В–∞—В –Љ—Л –њ–Њ–ї—Г—З–Є–ї–Є?
–Р —А–µ–Ј—Г–ї—М—В–∞—В —Б–≤–Њ–і–Є—В—Б—П –≤–Њ—В –Ї —З–µ–Љ—Г: —А–µ–Ј—Г–ї—М—В–∞—В—Л —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞ –Љ–Њ–≥—Г—В –љ–µ —П–≤–ї—П—В—М—Б—П –±–µ–Ј—Г—Б–ї–Њ–≤–љ—Л–Љ –Є –Њ–і–љ–Њ–Ј–љ–∞—З–љ—Л–Љ –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ–Љ –Є–ї–Є –Њ–њ—А–Њ–≤–µ—А–ґ–µ–љ–Є–µ–Љ –≥–Є–њ–Њ—В–µ–Ј—Л, –љ–Њ –Њ–љ–Є –Т–°–Х–У–Ф–Р —П–≤–ї—П—О—В—Б—П —Д–∞–Ї—В–Њ—А–Њ–Љ, –≤–ї–Є—П—О—Й–Є–Љ –љ–∞ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Є—Б—В–Є–љ–љ–Њ—Б—В–Є —Н—В–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л. –Я—А–Є—З–µ–Љ, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Њ—З–µ–љ—М –љ–µ–Љ–љ–Њ–≥–Њ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ–Њ–≥–Њ –Љ–∞—В–µ—А–Є–∞–ї–∞, —З—В–Њ–±—Л –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Є—Б—В–Є–љ–љ–Њ—Б—В–Є –љ–µ–Ї–Њ—В–Њ—А–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л —Б—В–∞–ї–∞ —А–∞–≤–љ–Њ–є (–Є–ї–Є –њ–Њ—З—В–Є —А–∞–≤–љ–Њ–є) –љ—Г–ї—О.
–Т –њ—А–Є–Љ–µ—А–µ —Б –Ї–Њ—А–Њ–≤–∞–Љ–Є –≥–Є–±–µ–ї—М –њ–Њ–і–Њ–њ—Л—В–љ—Л—Е –ґ–Є–≤–Њ—В–љ—Л—Е –Љ–Њ–ґ–љ–Њ –Њ–±—К—П—Б–љ–Є—В—М –Ї–∞–Ї –љ–µ—Б–њ–Њ—Б–Њ–±–љ–Њ—Б—В—М—О –Є—Е –Ї –њ–Њ–ї–µ—В—Г(–≤ —А–∞–Љ–Ї–∞—Е –Њ–і–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л), —В–∞–Ї –Є —В—А–µ—В—М–Є–Љ–Є –њ—А–Є—З–Є–љ–∞–Љ–Є( –≤ —А–∞–Љ–Ї–∞—Е –і—А—Г–≥–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л). –°–Є–ї–∞ –≥–Є–њ–Њ—В–µ–Ј—Л –Њ –љ–µ—Б–њ–Њ—Б–Њ–±–љ–Њ—Б—В–Є –Ї–Њ—А–Њ–≤ –ї–µ—В–∞—В—М –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ —В–Њ–Љ, —З—В–Њ –Њ–љ–∞ –љ–µ –і–Њ–њ—Г—Б–Ї–∞–µ—В –љ–µ–Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ–є —В—А–∞–Ї—В–Њ–≤–Ї–Є —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л—Е —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤. –Ш–Љ–µ–љ–љ–Њ —Н—В–∞ –Њ—Б–Њ–±–µ–љ–љ–Њ—Б—В—М –і–∞–љ–љ–Њ–є –≥–Є–њ–Њ—В–µ–Ј—Л –њ—А–Є–≤–Њ–і–Є—В –Ї –≤–Ј—А—Л–≤–љ–Њ–Љ—Г –њ–Њ–≤—Л—И–µ–љ–Є—О –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є –µ–µ –Є—Б—В–Є–љ–љ–Њ—Б—В–Є –≤ —Е–Њ–і–µ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞. –Ь–µ–ґ–і—Г –њ—А–Њ—З–Є–Љ, –і–∞–љ–љ—Л–є —А–µ–Ј—Г–ї—М—В–∞—В –µ—Б—В—М –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞—П –Є–ї–ї—О—Б—В—А–∞—Ж–Є—П –Є–Ј–≤–µ—Б—В–љ–Њ–≥–Њ –Ј–∞—П–≤–ї–µ–љ–Є—П –Љ–Є—Б—В–µ—А–∞ –®.–•–Њ–ї–Љ—Б–∞:
"–Ю—В–±—А–Њ—Б—М—В–µ –≤—Б–µ –љ–µ–≤–Њ–Ј–Љ–Њ–ґ–љ–Њ–µ, –Є —В–Њ, —З—В–Њ –Њ—Б—В–∞–љ–µ—В—Б—П, –±—Г–і–µ—В –Њ—В–≤–µ—В–Њ–Љ, –Ї–∞–Ї –±—Л –љ–µ–≤–µ—А–Њ—П—В–µ–љ –Њ–љ –љ–Є –Ї–∞–Ј–∞–ї—Б—П"
–Х—Б–ї–Є –≥–Є–њ–Њ—В–µ–Ј–∞ –Є—Б—В–Є–љ–љ–∞, —В–Њ –љ–∞—З–∞–ї—М–љ–∞—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –µ–µ –Є—Б—В–Є–љ–љ–Њ—Б—В–Є –Љ–Њ–ґ–µ—В –±—Л—В—М —Б–Ї–Њ–ї—М —Г–≥–Њ–і–љ–Њ –Љ–∞–ї–∞ - –≤ —Е–Њ–і–µ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Њ–≤ –≤—Б–µ –і—А—Г–≥–Є–µ –≥–Є–њ–Њ—В–µ–Ј—Л —Б—В–∞–љ—Г—В –µ—Й–µ –Љ–µ–љ–µ–µ –≤–µ—А–Њ—П—В–љ—Л.
–І—В–Њ –ґ. –Ґ–µ–њ–µ—А—М –Њ–±—А–∞—В–Є–Љ—Б—П –Ї —Б–њ–Њ—А—Г –≤–µ—А—Г—О—Й–Є—Е –Є –Љ–∞—В–µ—А–Є–∞–ї–Є—Б—В–Њ–≤. –Т—А—П–і –ї–Є –Ї—В–Њ-–ї–Є–±–Њ —Б—В–∞–љ–µ—В —Г—В–≤–µ—А–ґ–і–∞—В—М, —З—В–Њ —Б—Г—Й–µ—Б—В–≤—Г—О—В –±–µ–Ј—Г—Б–ї–Њ–≤–љ—Л–µ –Є –Њ–і–љ–Њ–Ј–љ–∞—З–љ—Л–µ –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–∞ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П –С–Њ–≥–∞. –Х—Б–ї–Є –±—Л –Њ–љ–Є —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–ї–Є, –Љ–∞—В–µ—А–Є–∞–ї–Є—Б—В–Є—З–µ—Б–Ї–∞—П –≥–Є–њ–Њ—В–µ–Ј–∞ –±—Л–ї–∞ –±—Л –љ–µ–Љ–µ–і–ї–µ–љ–љ–Њ –Њ–њ—А–Њ–≤–µ—А–≥–љ—Г—В–∞, –Є —Б–њ–Њ—А–Є—В—М –±—Л –±—Л–ї–Њ –љ–µ –Њ —З–µ–Љ.
–Т –Ї–∞—З–µ—Б—В–≤–µ –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П –С–Њ–≥–∞, –Ї–∞–Ї –њ—А–∞–≤–Є–ї–Њ, –њ—А–Є–≤–Њ–і—П—В—Б—П –њ—А–Є–Љ–µ—А—Л, –і–Њ–њ—Г—Б–Ї–∞—О—Й–Є–µ –љ–µ–Њ–і–љ–Њ–Ј–љ–∞—З–љ—Г—О —В—А–∞–Ї—В–Њ–≤–Ї—Г. –Ь–∞—В–µ—А–Є–∞–ї–Є—Б—В–Є—З–µ—Б–Ї–∞—П –ґ–µ –њ–Њ–Ј–Є—Ж–Є—П, –љ–∞–њ—А–Њ—В–Є–≤, —В—А–∞–Ї—В—Г–µ—В –≤—Б–µ –љ–∞–±–ї—О–і–µ–љ–Є—П –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ. –Ъ–Њ–≥–і–∞ —А–µ–Ї–∞ —В–µ—З–µ—В –≤–љ–Є–Ј –њ–Њ–і –і–µ–є—Б—В–≤–Є–µ–Љ —Б–Є–ї—Л —В—П–ґ–µ—Б—В–Є, –Љ–∞—В–µ—А–Є–∞–ї–Є—Б—В –≥–Њ–≤–Њ—А–Є—В –Њ –і–µ–є—Б—В–≤–Є–Є –Ј–∞–Ї–Њ–љ–Њ–≤ –њ—А–Є—А–Њ–і—Л. –Ш –љ–µ—В –Њ—Б–љ–Њ–≤–∞–љ–Є–є –њ—А–µ–і–њ–Њ–ї–∞–≥–∞—В—М –Ј–і–µ—Б—М –±–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–µ –≤–Љ–µ—И–∞—В–µ–ї—М—Б—В–≤–Њ. –Х—Б–ї–Є –±—Л —А–µ–Ї–∞ –≤–і—А—Г–≥ –њ–Њ—В–µ–Ї–ї–∞ –±—Л –Т–Т–Х–†–•, —Н—В–Њ –±—Л–ї–Њ –±—Л –љ–µ—Б–Њ–Љ–љ–µ–љ–љ—Л–Љ —З—Г–і–Њ–Љ, –±–µ–Ј—Г—Б–ї–Њ–≤–љ–Њ –Њ–њ—А–Њ–≤–µ—А–≥–∞—О—Й–Є–Љ –Љ–∞—В–µ—А–Є–∞–ї–Є—Б—В–Є—З–µ—Б–Ї–Њ–µ –Љ–Є—А–Њ–≤–Њ–Ј–Ј—А–µ–љ–Є–µ –Є –њ–Њ–і—В–≤–µ—А–ґ–і–∞—О—Й–Є–Љ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є–µ –С–Њ–≥–∞. –Э–Њ –Ј–∞ –≤—Б—О –Є—Б—В–Њ—А–Є—О –Є–Ј—Г—З–µ–љ–Є—П —З–µ–ї–Њ–≤–µ—З–µ—Б—В–≤–Њ–Љ –њ—А–Є—А–Њ–і—Л, –њ–Њ–і–Њ–±–љ—Л—Е —З—Г–і–µ—Б –і–Њ–Ї—Г–Љ–µ–љ—В–∞–ї—М–љ–Њ –љ–µ –љ–∞–±–ї—О–і–∞–ї–Њ—Б—М.
–Ы–µ–≥–Ї–Њ –≤–Є–і–µ—В—М, —З—В–Њ —Б—Е–µ–Љ—Л "–С–Њ–≥ –µ—Б—В—М - –С–Њ–≥–∞ –љ–µ—В" –Є "–Ъ–Њ—А–Њ–≤—Л –ї–µ—В–∞—О—В - –Ї–Њ—А–Њ–≤—Л –љ–µ –ї–µ—В–∞—О—В" –∞–±—Б–Њ–ї—О—В–љ–Њ –Є–і–µ–љ—В–Є—З–љ—Л. –Х—Б—В–µ—Б—В–≤–µ–љ–љ–Њ, –Є–і–µ–љ—В–Є—З–љ–∞ –Є –і–Є–љ–∞–Љ–Є–Ї–∞ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В–µ–є –Є—Б—В–Є–љ–љ–Њ—Б—В–Є. –Р –њ–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ—А–Њ—Б—В–Њ–є –ґ–Є—В–µ–є—Б–Ї–Є–є –Њ–њ—Л—В –Ї–∞–ґ–і–Њ–≥–Њ –Є–Ј –љ–∞—Б –µ—Б—В—М –љ–µ–њ—А–µ—А—Л–≤–љ–Њ–є —Б–µ—А–Є–µ–є —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Њ–≤ —Б —Ж–µ–ї—М—О –Њ–±–љ–∞—А—Г–ґ–µ–љ–Є—П –±–Њ–ґ–µ—Б—В–≤–µ–љ–љ–Њ–≥–Њ –≤–Љ–µ—И–∞—В–µ–ї—М—Б—В–≤–∞, —В–Њ –њ–Њ—Б–ї–µ —Н—В–Є—Е —В—А–Є–ї–ї–Є–Њ–љ–Њ–≤ –Є —В—А–Є–ї–ї–Є–Њ–љ–Њ–≤ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Њ–≤ —П –Љ–Њ–≥—Г —Б–Ї–∞–Ј–∞—В—М:
–Э–µ —Д–∞–Ї—В, —З—В–Њ –С–Њ–≥–∞ –љ–µ—В. –Э–µ —Д–∞–Ї—В, —З—В–Њ –Њ–љ —Б—Г—Й–µ—Б—В–≤—Г–µ—В. –Э–Њ —В–Њ, —З—В–Њ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –µ–≥–Њ —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П —А–∞–≤–љ–∞ –љ—Г–ї—О —Б —В–Њ—З–љ–Њ—Б—В—М—О –і–Њ –Љ–Є–ї–ї–Є–∞—А–і–љ–Њ–≥–Њ –Ј–љ–∞–Ї–∞ –њ–Њ—Б–ї–µ –Ј–∞–њ—П—В–Њ–є - —Н—В–Њ —Д–∞–Ї—В.